The source text is taken from here: http://www.math.stonybrook.edu/~tony/mazes/levelseq.html
Математикаға арналған 
лабиринттер арқылы
Қарапайым, ауыспалы транзиттік лабиринттерді математикалық тұрғыдан зерттеуге мүмкіндік беретін негізгі факт мыналар болып табылады. Қарапайым, ауыспалы транзиттік лабиринттің топологиясы оның деңгейлік реттілігімен толығымен анықталады. Мұның қалай жұмыс істейтіні төменде түсіндіріледі; бұл дегеніміз, егер екі отырғызылған лабиринттің (айталық, екеуі де жазылмаған түрде) бірдей деңгейлік дәйектілігі болса, онда біреуін екіншісіне немесе екіншісінің айна бейнесіне сәйкес етіп өзгерте отырып, деңгейдің сақталуын үздіксіз өзгерте аламыз.
Бұдан шығатыны, қарапайым ауыспалы транзиттік лабиринттердің толық топологиялық жіктемесі сандардың қандай тізбектері деңгейлік тізбектер ретінде пайда болатындығын анықтауға жетеді, ал шын мәнінде 0-ден n-ге дейінгі сандардың орнын ауыстыру үшін қажетті және жеткілікті үш шарт бар n тереңдіктегі лабиринттің деңгейлік реттілігі.
1. Реттік 0-ден басталып, n-мен аяқталуы керек.
2. Тақ және жұп сандар кезектесіп ауысуы керек.
3. Жұп саннан басталатын деңгей тізбегіндегі қатарлы сандардың жұптарын қарастырыңыз; бұл лабиринттің оң жағындағы тік бөліктерге сәйкес келеді. (*) Егер осы сегменттердің екеуі қабаттасса, біреуі екіншісінің ішінде орналасуы керек. Тақ саннан басталатын жұптар үшін де солай болуы керек; бұлар сол жақтағы тік жол кесінділеріне сәйкес келеді.
Мысал: Константинополь лабиринтінің деңгейлік реттілігінде (10,1) және (2,11) сегменттері қабаттасады, бірақ екіншісінде де орналаспайды; сондықтан бұл лабиринттің деңгейлік реттілігі бола алмайды.
Міне, бұл қалай дәлелденді. 1 қажеттілігі: айқын. 2-нің қажеттілігі: Айталық, оң жақта тік кесіндімен жалғасқан екі қатарлы қабат, мысалы, бірдей паритетке ие болсын делік; олардың арасындағы кеңістіктің тақ саны болуы керек. Сол кеңістіктен өтетін кез-келген жол сол жаққа кіріп-шығуы керек, сондықтан деңгейлердің жұп санын ғана қолдана алады. Қарама-қайшылық. 3 қажеттілігі: лабиринтті жазба түрінде, кіреберісімен, айталық, оң жағымен ойлаңыз. Жол 0 деңгейден оң жағынан басталып, тақ деңгейге дейін төмендейді. Содан кейін ол солға өтіп, реттіліктің келесі деңгейіне ауысады, ол біркелкі болады, содан кейін оңға және т.с.с. Сонымен, жұп саннан басталатын деңгей тізбегіндегі тізбектелген сандардың жұптары тікке сәйкес келеді лабиринттің оң жағындағы сегменттер, ал тақ саннан басталатындар сол жақ сегменттерге дейін. Енді оң жақта орналасқан кез-келген тік жол кесінділерін қарастырыңыз. Егер олар қабаттасса, онда екіншісінің ішіне ұя салу керек. Әйтпесе, екеуі де көлденең кесінділермен сол жаққа қосыла алмады, өйткені лабиринт жолы өзін қиып өте алмайды; сол жақтағы тік жол сегменттері үшін де солай болуы керек.
Жетістік: 1, 2 және 3 шарттарын қанағаттандыратын 0-ден n-ге дейінгі бүтін сандарға ауыстыру берілсін делік. Оны лабиринтке айналдыру әдісі. Қапталған қағазға сызықтарды жоғарыдан бастап 0-ден n-ге дейін нөмірлеңіз. Жұп саннан басталатын тізбектегі тізбектегі кезекті жұптардың әрқайсысы үшін парақтың оң жағында тік кесіндісімен сәйкесінше нөмірленген жолдарды қосыңыз. Егер осы сегменттердің екеуі ұяға салынған болса, ұзыннан солға қысқасын салыңыз. Енді сол жақтан басқа тақ басталатын жұптармен дәл солай жасаңыз, қысқа сегменттерді оң жаққа орналастырыңыз. Енді 1,…,n-1 нөмірленген жолдардың әрқайсысында фигураның екі бос шеті болады. Оларды сол сызық бойымен қосыңыз; бұл жоғарғы және төменгі жағында бос ұш қалдырады. Сіз Ариадна жіптерін қ.а.т.-ның жайылған түрімен сызған боласыз. сіз бастаған деңгейлік реттілікке сәйкес лабиринт. Енді лабиринттің өзін сызу оңай. Сонымен қатар, лабиринттің сол бөлігін парақтың оң және сол жақ шеттеріне жақындастыру және осы екі бөлікті олардың сыртқы тіректері бойынша біріктіру, шиыршықталған пішінді алуға болатын ядро жасайды.
Тони Филлипс/Tony Phillips
Математика бөлімі SUNY Stony Brook
tony at math.stonybrook.edu
5 маусым 2018 ж
Бұл лабиринттердің ішіндегі ең танымалсы – Крит лабиринті. Оны 
Міне, тағы бір мысал. Бұл лабиринт бірнеше ортағасырлық еврей 
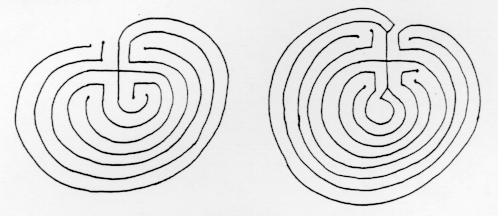ТРАНЗИТТІК лабиринттері, өйткені жол лабиринттің сыртынан орталыққа қарай бифуркациясыз өтеді. Мысалы, бұл лабиринттер транзиттік лабиринттер емес: біреуінде жол сол кірген жағынан шығады; ал екіншісінде лабиринт жүгірушінің қай жолмен жүретінін таңдау керек нүктелері бар.
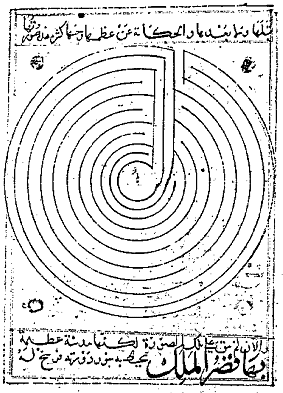АУЫСПАЛЫ, өйткені лабиринттің жоспары белгілі бір концентрлі немесе параллель деңгейлерде салынған және лабиринт жолы деңгей өзгерген сайын бағытын өзгертеді. Мысалы, бұл лабиринт, ортағасырлық араб географиясы кітабындағы Константинополь жоспарын бейнелейтін, оның деңгейі әр түрлі, бірақ ауыспалы емес, өйткені ол бағытты өзгертпестен 10-деңгейден 1-деңгейге айналады. Оның деңгейлік дәйектілігі 0.3.4.5.6.7.8.9.10.1.2.11 мүмкін емес, біз көріп отырғанымыздай, ауыспалы лабиринттің 
КАРАПАЙЫМ, өйткені жол әр деңгейде толық шеңбер жасайды; атап айтқанда, ол әр деңгейде дәл бір рет жүреді. Мысалы, Чартрде (мұнда көрсетілген) және басқа бірнеше соборларда тротуар лабиринті ретінде кездесетін және Луккадағы собордағы бағанға ойылған бұл ауыспалы транзиттік лабиринт қарапайым емес: жолдың төрт түрлі нүктесі бар деңгейлерін өзгерте алады. Бұл лабиринт хрестяндық крит дизайнын және оның римдік ұрпақтарын жетілдіру және күшейту ретінде пайда болған сияқты; Тезес мифімен байланысы сақталды. Жаңа дизайн өзінің табандылығымен ерекшеленді. 9 ғасырдан бастап ортағасырлық қолжазбаларда кездеседі; Шартр соборы 1200 жылы салынды; және 16 ғасырдың басында бірдей өрнек 